Graph Theory

---

Eulerian Trails

Definition

If the graph $G$ has the property that for any two vertices $x$ and $y$, one can find a path from $x$ and $y$, then we say that $G$ is a connected graph.

Definition

If a graph $G$ has no loops and has no multiple edges between the same pair of points, then we will say that $G$ is a simple graph.

Definition

A sequence of distinct edges $e_1e_2 \cdots e_k$ is called a trail if we can take a continuous walk in our graph. A walk is like a trail, except that all edges do not need to be distinct.

If a trail uses all edges of $G$, then we call it an Eulerian trail. If a trail does not touch any vertex twice, then we call it a path.

Theorem

A connected graph $G$ has a closed Eulerian trail if and only if all vertices of $G$ have an even degree.

Proof

First, we prove the "only if" part, that is, we show that if $G$ has a closed Eulerian trail, then all vertices of $G$ must have an even degree. Indeed, when we take the closed Eulerian trail $W$, we visit each vertex a certain number of times. Let $A$ be a vertex that was not where $W$ started, and assume we visited $A$ exactly $a$ times. This means we entered $A$ exactly $a$ times, and we left $A$ exactly $a$ times. As we assumed $W$ was a trail, we had to do this using different edges, so we used $2 a$ edges. On the other hand, $W$ contains all edges of $G$, so $A$ cannot have any additional edges, therefore the degree of $A$ is $2 a$. This shows that the degree of any vertex other than the starting point $S$ of $W$ is even. Finally, note that $S$ is not only the starting point of $W$, but also the endpoint, so if we visit $S$ exactly $t$ times between the start and the end of $W$, then we use $1+2 t+1=2(t+1)$ edges. Therefore, the degree of $S$ is $2(t+1)$, and our claim is proved.

Now let us assume that all vertices of $G$ have an even degree and prove that $G$ has a closed Eulerian trail. Take any vertex $S$, and start walking along an edge $e_1$, to the other endpoint $A_1$ of that edge, then walk along any new edge $e_2$ that starts in $A_1$. Continue this way, using new (previously unused) edges at each step, until a closed trail $C_1$ is formed. As $G$ is finite, such a closed trail will always be formed. The first closed trail will be formed when we first revisit a vertex already visited. We cannot get stuck at some vertex before completing a closed trail as each vertex has an even degree, so each time we enter a vertex, we can also leave it, except possibly the initial vertex. If $C_1=G$, then we are done. If not, then choose a vertex $V$ in $C_1$ so that $C_1$ does not contain all edges adjacent to $V$.

The alert reader can ask now how we know that there is such a vertex $V$. Let us assume that there is not. As $C_1$ contains fewer edges than $G$, and supposedly $C_1$ contains all edges adjacent to all vertices it contains, there must be a vertex $A$ that is not in $C_1$. However, $G$ is a connected graph, so there must be a path connecting $A$ to any vertex in $C_1$. Start walking on this path from $A$ to any given vertex of $C_1$. When you reach $C_1$ the first time, you will reach it in a vertex $V$ that is in $C_1$, but not all the edges adjacent to it are in $C_1$. Indeed, the one that has just ended in $V$ is not. This proves by contradiction that such a vertex $V$ always exists. Illustrated here:

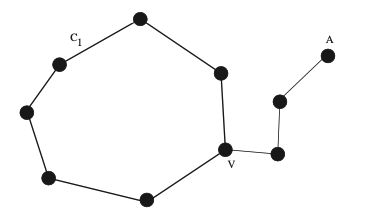
Let us now remove all edges of $C_1$ from $G$. We get a graph in which again all vertices have an even degree. Starting at $V$, let us take another closed trail $C_2$ in the remaining graph. We can then unite $C_1$ and $C_2$ into one closed trail in $G$. Indeed, if we start walking by $C_1$, we can stop at $V$, walk through $C_2$, then complete our trail by using the remaining part of $C_1$. If the new trail $C_1 \cup C_2$ contains all edges of $G$, we are done. If not, then let us omit $C_1 \cup C_2$ from $G$, and find a new closed trail $C_3$ in the remaining graph.

As $G$ has a finite number of edges, this procedure has to stop after a finite number of steps. Therefore, after a finite number of steps, $C_1 \cup C_2 \cup \cdots \cup C_k$ will be a closed trail containing all edges of $G$.

---

Hamiltonian Cycles

Definition

A cycle in a graph is a closed trail that does not touch any vertex twice, except, the initial vertex, which must also be the ending vertex. A cycle that includes all vertices of a graph is called a Hamiltonian path.

Theorem

Let $n \geq 3$, let $G$ be a simple graph on $n$ vertices, and let us assume that all vertices in $G$ are of degree at least $n / 2$. Then $G$ has a Hamiltonian cycle.

Proof

Note that it follows from the conditions that $G$ is connected. Indeed, if $G$ had more than one component, then it would have a component of less than $n / 2$ vertices, and vertices in that component would have a degree less than $n / 2$.

Let us assume that $G$ does not have a Hamiltonian cycle. Let us add new edges to $G$ as long as we can without creating a Hamiltonian cycle. When we stop, we have a graph $G^{\prime}$ in which all vertices have a degree at least $n / 2$, there is no Hamiltonian cycle, but adding any new edge would create a Hamiltonian cycle.

Let $P$ be a path of maximum length in $G^{\prime}$. We claim that $P$ contains all vertices of $G^{\prime}$. Indeed let $x$ and $y$ be two vertices in $G^{\prime}$ that are not connected by an edge. As adding the edge $x y$ would create a Hamiltonian cycle, it follows that $G^{\prime}$ has a Hamiltonian path $P$ that starts at $x$ and ends $\operatorname{in} y$.

Let $x=z_1, z_2, z_3, \cdots, z_{n-1}, z_n=y$ be the vertices of this path, from $x$ to $y$. Vertices $x$ and $y$ together have at least $n$ neighbors. Therefore, the Pigeon-hole Principle implies that there must be an index $i$ so that $2 \leq i \leq n-1$, while $x z_i$ is an edge, and also, $z_{i-1} y$ is an edge. (Otherwise the set of neighbors of $y$ and the set of vertices that immediately precede a neighbor of $x$ on the $x y$-path would be disjoint, which is impossible since these sets are too large.) This is a contradiction, however, for this would mean that $x z_2 \cdots z_{i-1} y z_{n-1} \cdots z_i$ is a Hamiltonian cycle as shown below.

---

Directed Graphs

Definition

A graph in which each edge is assigned a direction is called a directed graph or digraph.

Theorem 1

A directed graph $G$ has a closed Eulerian trail if and only if it is balanced and strongly connected.

Proof

First, we prove that these conditions are necessary. As a closed Eulerian trail $W$ leaves each vertex as many times as it enters that vertex, $G$ must be balanced. Similarly, $W$ provides a trail from any vertex to any vertex, so $G$ is strongly connected.

Theorem 2

All tournaments have a Hamiltonian path. Proof. We prove the claim by induction on $n$, the number of vertices of our tournament $T$. If $T$ has one, or two vertices, then the statement is clearly true. Now assume that we know the statement for all tournaments having $n-1$ vertices. Let $T$ be any tournament on $n$ vertices. Separate any vertex $V$, and call the remaining graph on $n-1$ vertices $T^{\prime}$. By the induction hypothesis, $T^{\prime}$ has a Hamiltonian path $h=h_1 h_2 \cdots h_{n-1}$. The question is how we can insert $V$ into $h$. If there is an index $i$ so that $h_i V$ is an edge and $V h_{i+1}$ is an edge, then we can insert $V$ between $h_i$ and $h_{i+1}$. If no such $i$ exists, then there must exist an index $k$ so that $0 \leq k \leq n-1$, and for all $j \leq k, V h_j$ is an edge, and for all $j>k, h_j V$ is an edge. Therefore, either $V h_1$ is an edge, or $h_{n-1} V$ is an edge. So we can affix $V$ either to the front or to the end of $h$.

Theorem 3

A tournament $T$ has a Hamiltonian cycle if and only if it is strongly connected.

Proof

If $T$ has a Hamiltonian cycle, then that cycle provides a directed path from any vertex to any vertex, so $G$ is strongly connected.

Now let us assume that $T$ is strongly connected, and let $E(T)$ denote the set of edges of $T$. First, we prove that $T$ does contain a cycle. Indeed, if it did not, then $x y \in E(T)$ and $y z \in E(T)$ would imply $x z \in E(T)$, so $T$ would be a transitive tournament. In such a tournament, the vertices can be listed from left to right so that $i j \in E(T)$ if and only if $j$ is on the right of $i$. However, such a tournament is not strongly connected as no paths go to the right. So $T$ does have a cycle.

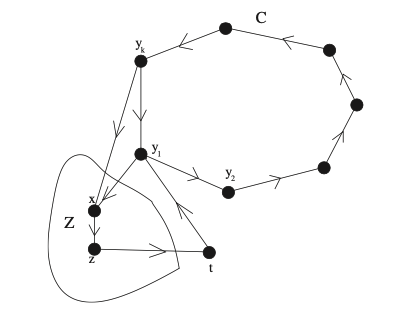
Let $C=y_1 y_2 \cdots y_k$ be a cycle of maximal length in $T$, and assume $C$ is not a Hamiltonian cycle. As $T$ is strongly connected, it contains an edge from $C$ to some vertex $x$ that is not in $C$. We can assume without loss of generality that this edge is $y_1 x$. If $x y_2$ were an edge, then $y_1 x y_2 y_3 \cdots y_k$ would be a cycle having more vertices than $C$. Therefore, $y_2 x$ has to be an edge, and then similarly, $y_3 x, y_4 x, \cdots, y_k x$ must all be edges.

Let $Z$ be the set of all vertices $z$ so that $y_1 z \in E(T)$. Then $y_i z \in E(T)$ for all $z \in Z$ and all $i \in[k]$ by the same argument as the one we applied for $y_i x$ in the previous paragraph. Let $z t$ be an edge, with $z \in Z$, and $t \notin Z$. Such an edge exists as $T$ is strongly connected. Then $t \notin C$, and therefore $t \notin Z$ implies that $t y_1 \in E(T)$. Then, however, $z t y_1 y_2 y_3 \cdots y_k$ is a longer cycle than $C$. The figure below shows our construction. This contradiction completes the proof.

---

Isomorphisms

Definition

We say that graphs $G$ and $H$ are isomorphic if there is a bijection $f$ from the vertex set of $G$ onto that of $H$ so that the number of edges between any pair of vertices $X$ and $Y$ of $G$ is equal to the number of edges between vertices $f(X)$ and $f(Y)$ of $H$. The bijection $f$ is called an isomorphism.