Backward Reachable Tube
Problem 1
The unsafe set in this case is just the failure set itself. This is because, at the edge of the failure set, we can instantly change the heading away from it, bringing us away from the failure set.
If the failure set is our target set:
We can reach the goal set anywhere because we can just set the heading toward it. Therefore, we expect our "unsafe set" to be infinitely big. Here, in our program, we run for 2 seconds at the speed of 1 m/s. Therefore, we expect the gap to be 2 meters from the target st.
Problem 2
Maximize value function (going away from the failure set):
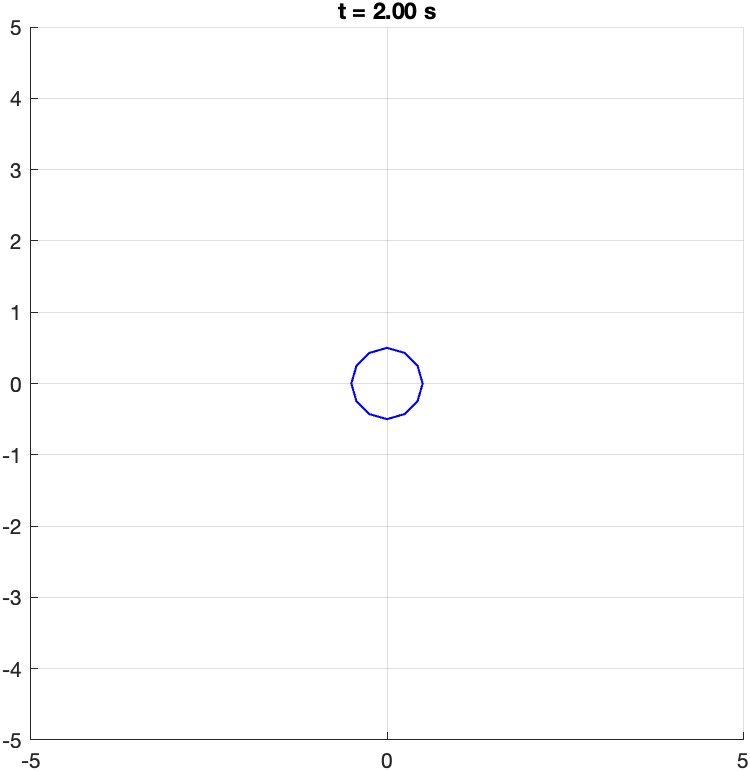
Minimize value function (going into the target set):
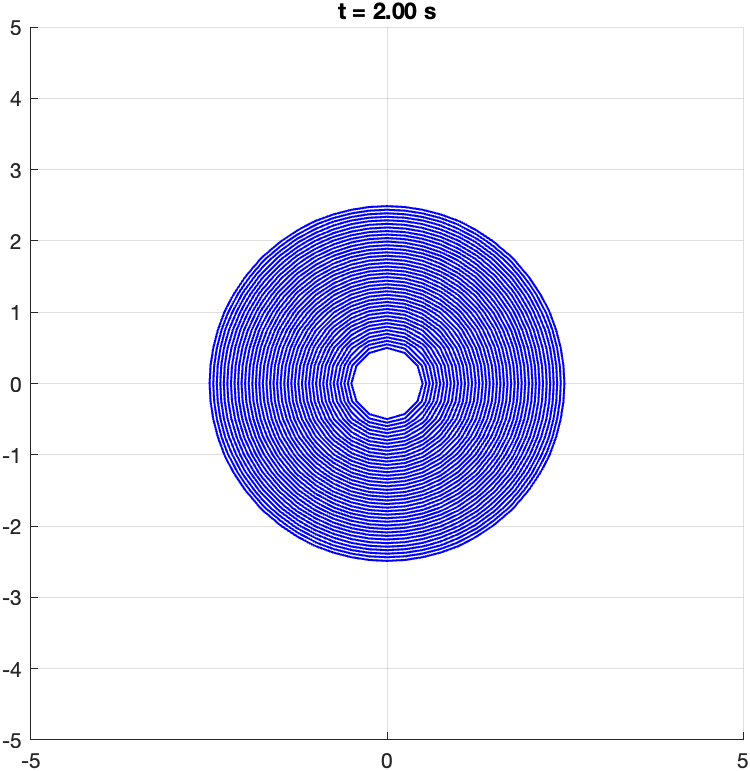
This aligns perfectly with my analytical computation.
Code
%% TODO
% Compute the optimal control
if strcmp(uMode, 'max')
uOpt = atan2(deriv{obj.dims==2}, deriv{obj.dims==1});
elseif strcmp(uMode, 'min')
uOpt = atan2(deriv{obj.dims==2}, deriv{obj.dims==1})-pi;
else
error('Unknown uMode!')
end
Problem 3
Part 1
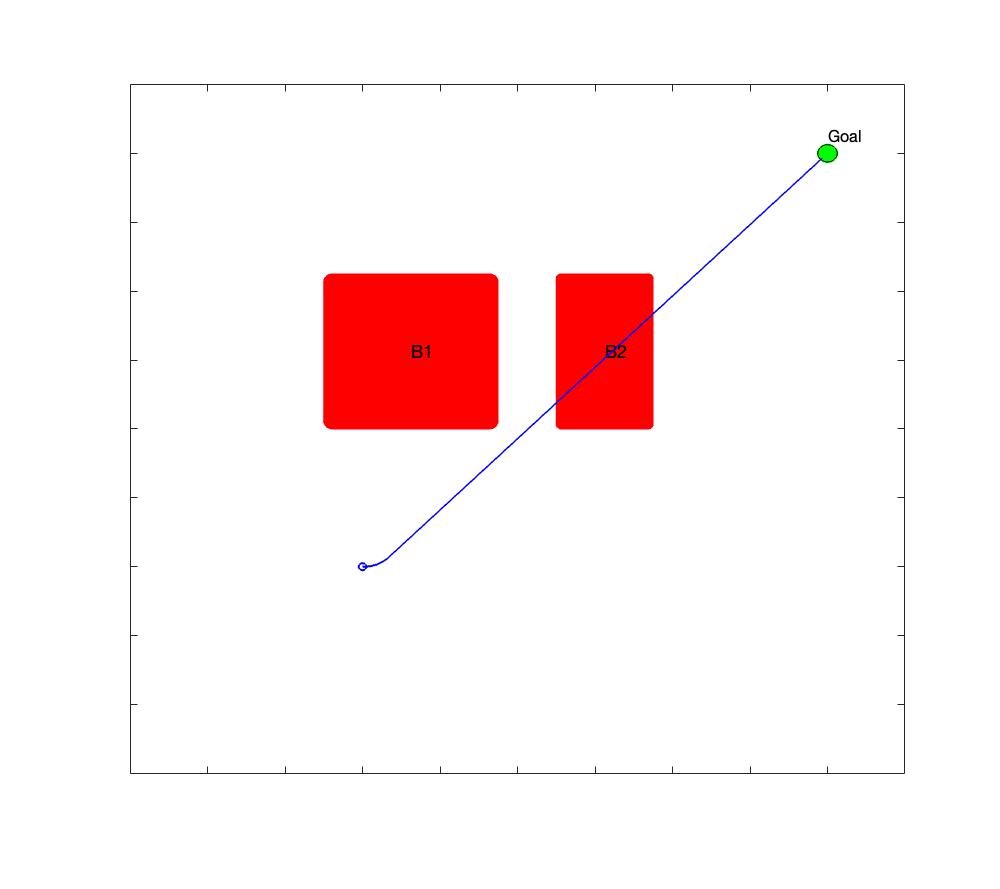
Part 2
BRT_computation.m
%% TODO
% Define the grid for the computation: g
grid_min = [-10; -10; -pi]; % Lower corner of computation domain
grid_max = [10; 10; pi]; % Upper corner of computation domain
N = [51; 51; 51]; % Number of grid points per dimension
pdDims = 3; % 3rd dimension is periodic
g = createGrid(grid_min, grid_max, N, pdDims);
%% TODO
% Define the failure set: data0
data0 = shapeUnion(shapeRectangleByCorners(g, [obsX1; obsY1; -inf], ...
[obsX1+width1; obsY1+height1; inf]), shapeRectangleByCorners(g, [obsX2; obsY2; -inf],...
[obsX2+width2; obsY2+height2; inf]));
optCtrl.m
if strcmp(uMode, 'max')
uOpt = (deriv{3}>=0)*obj.wRange(2) + (deriv{3}<0)*(obj.wRange(1));
elseif strcmp(uMode, 'min')
uOpt = (deriv{3}>=0)*(obj.wRange(1)) + (deriv{3}<0)*obj.wRange(2);
else
error('Unknown uMode!')
end
optDstb.m
theta = atan2(-deriv{2}, -deriv{1});
dOpt{1} = obj.dMax * cos(theta);% Compute the optimal disturbance in x
dOpt{2} = obj.dMax * sin(theta);% Compute the optimal disturbance in y
Heading:
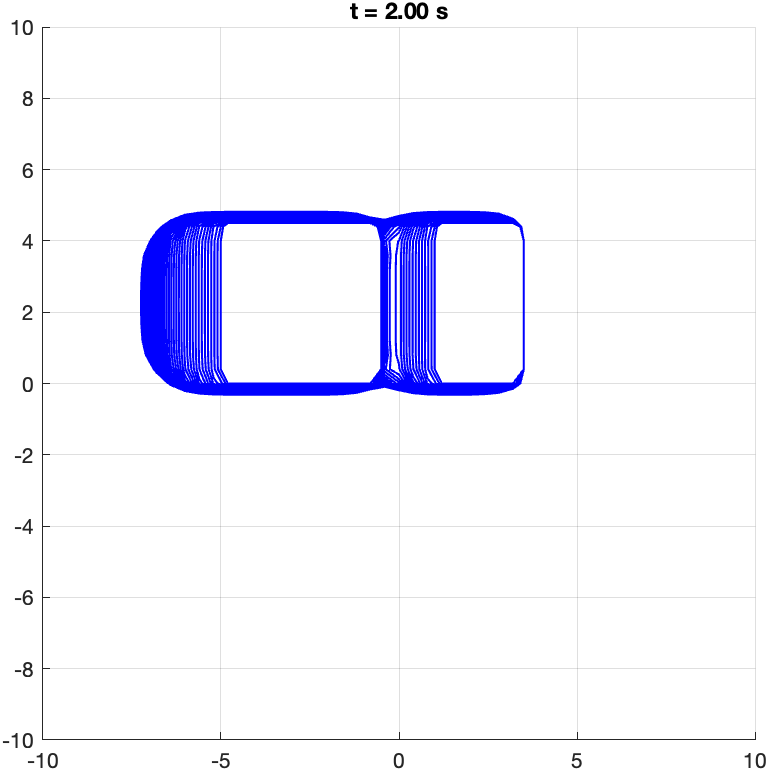
Heading:
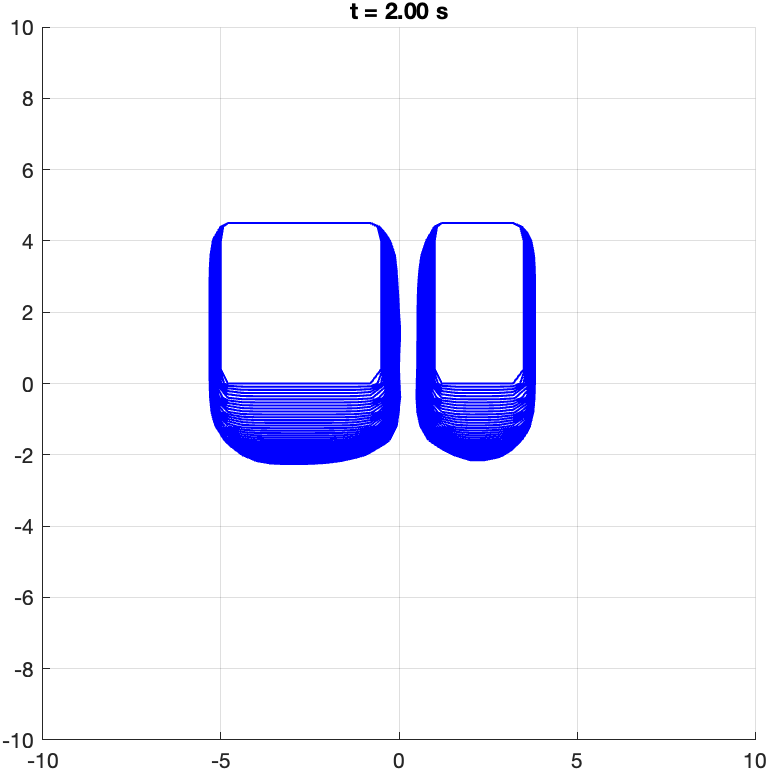
Heading:
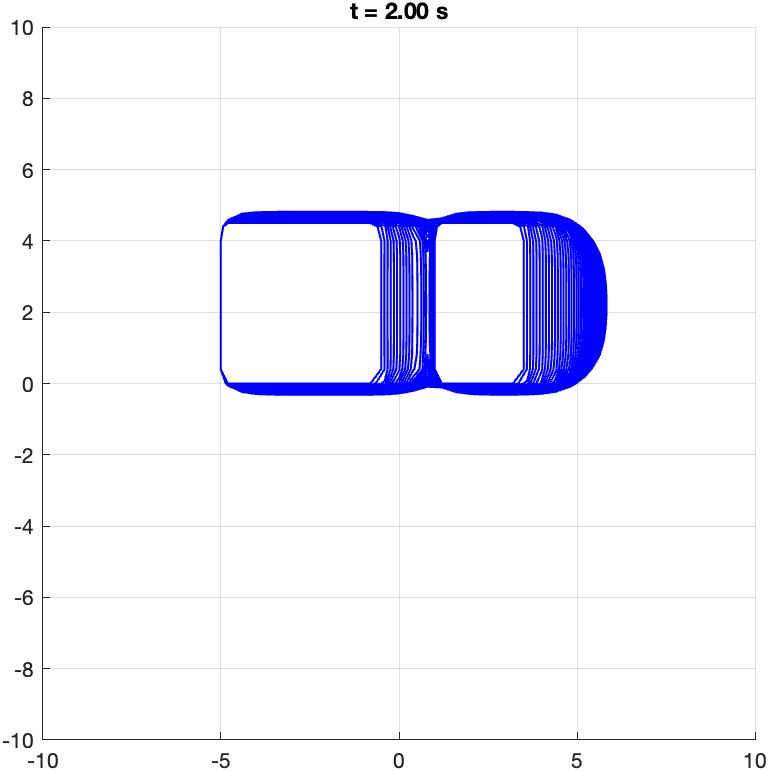
Heading:
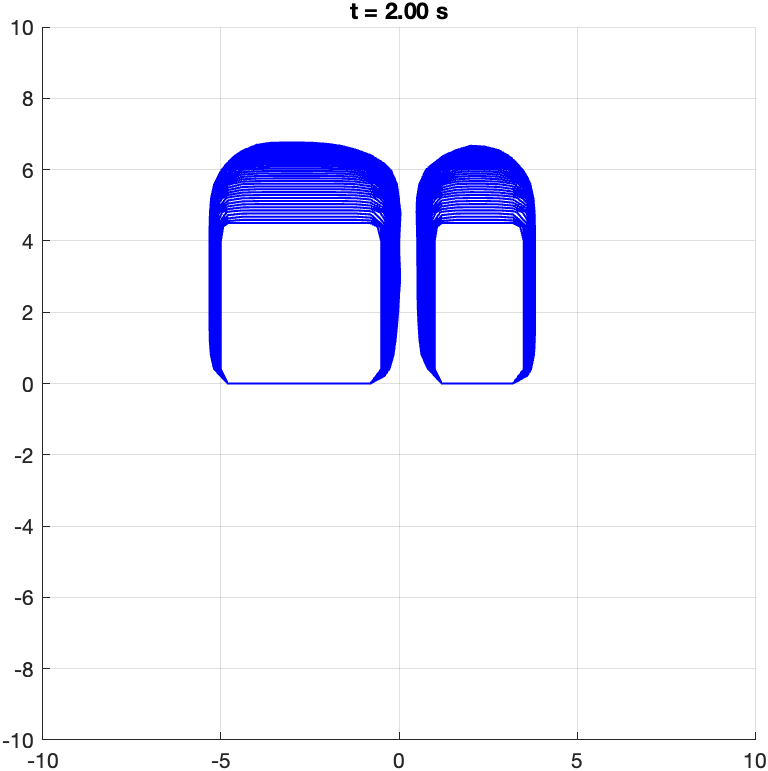
Part 3
Test case 4
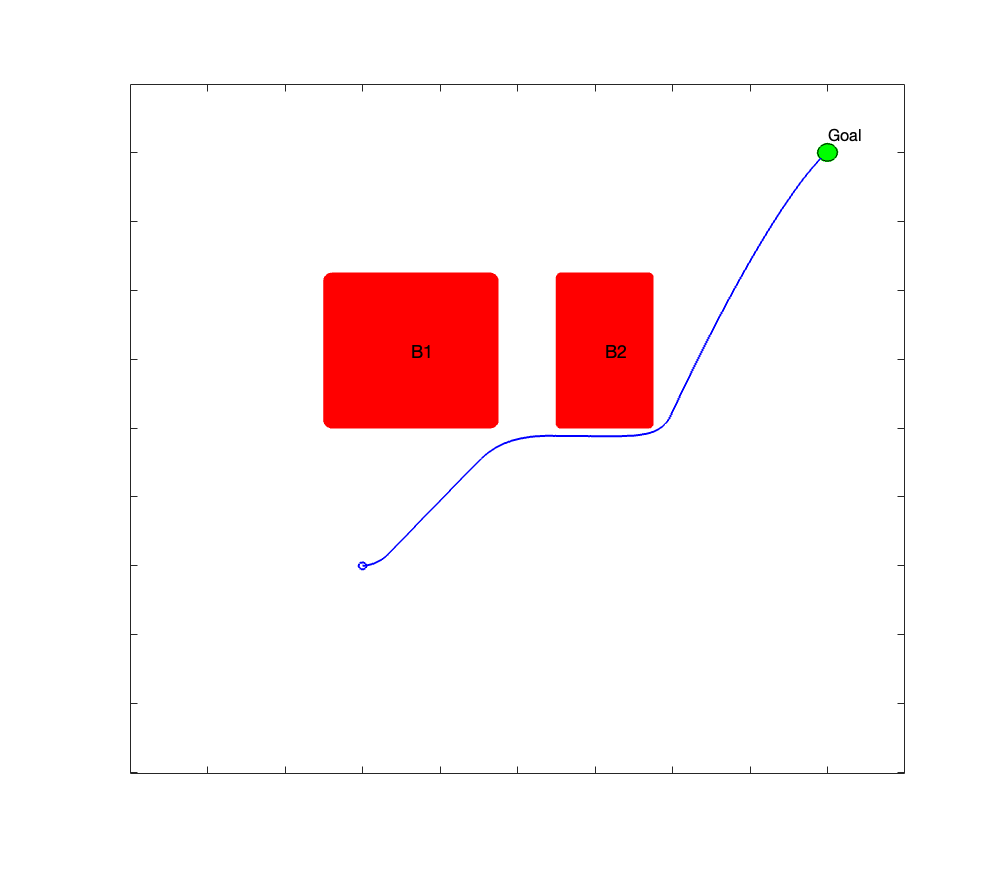
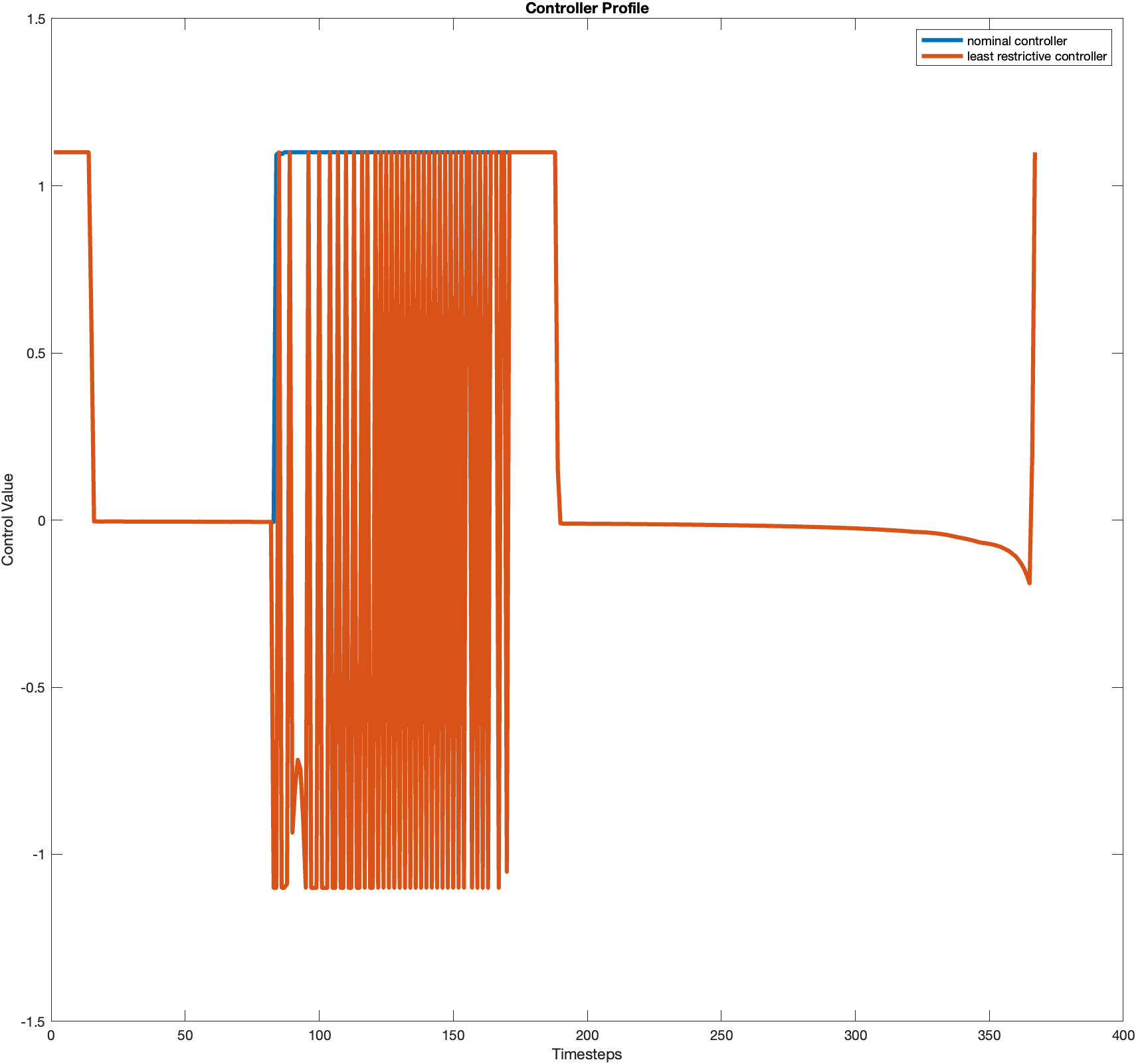
Test case 5
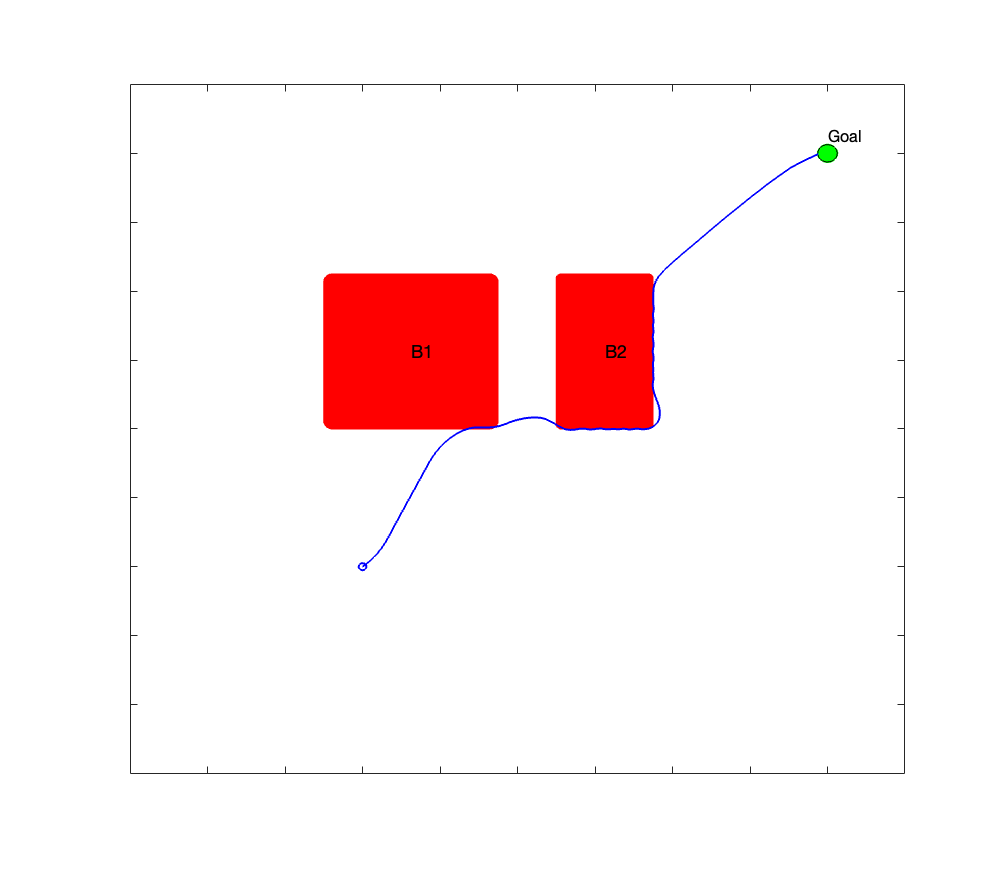
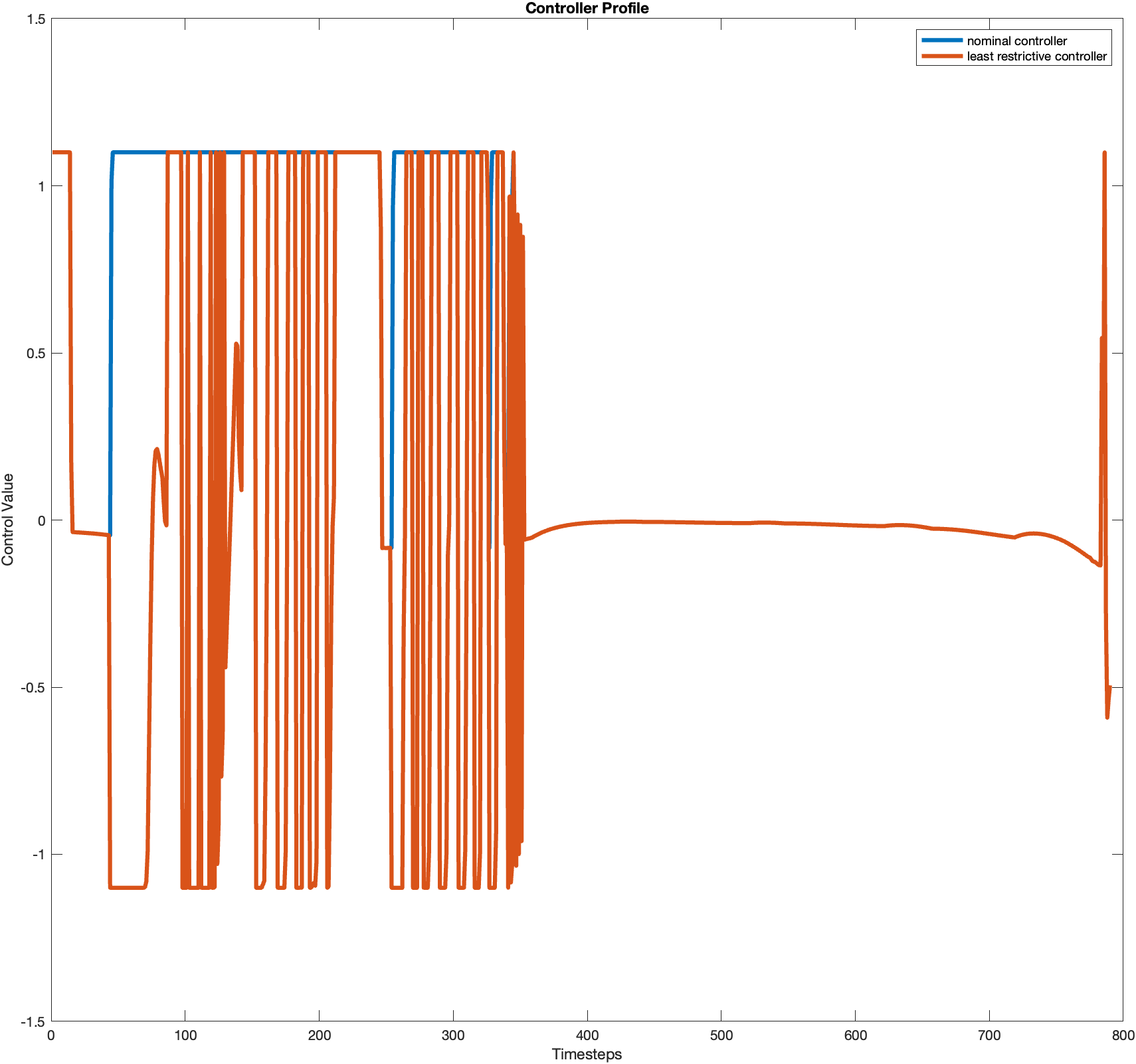
Least-restrictive Code
if (eval_u(params.g,params.data(:,:,:,end),x_curr) <= 0) % the system will end in unsafe state!
u_filtered = eval_u(params.g,params.safety_controller,x_curr); % get safety controller
else
u_filtered = u_nom;
end
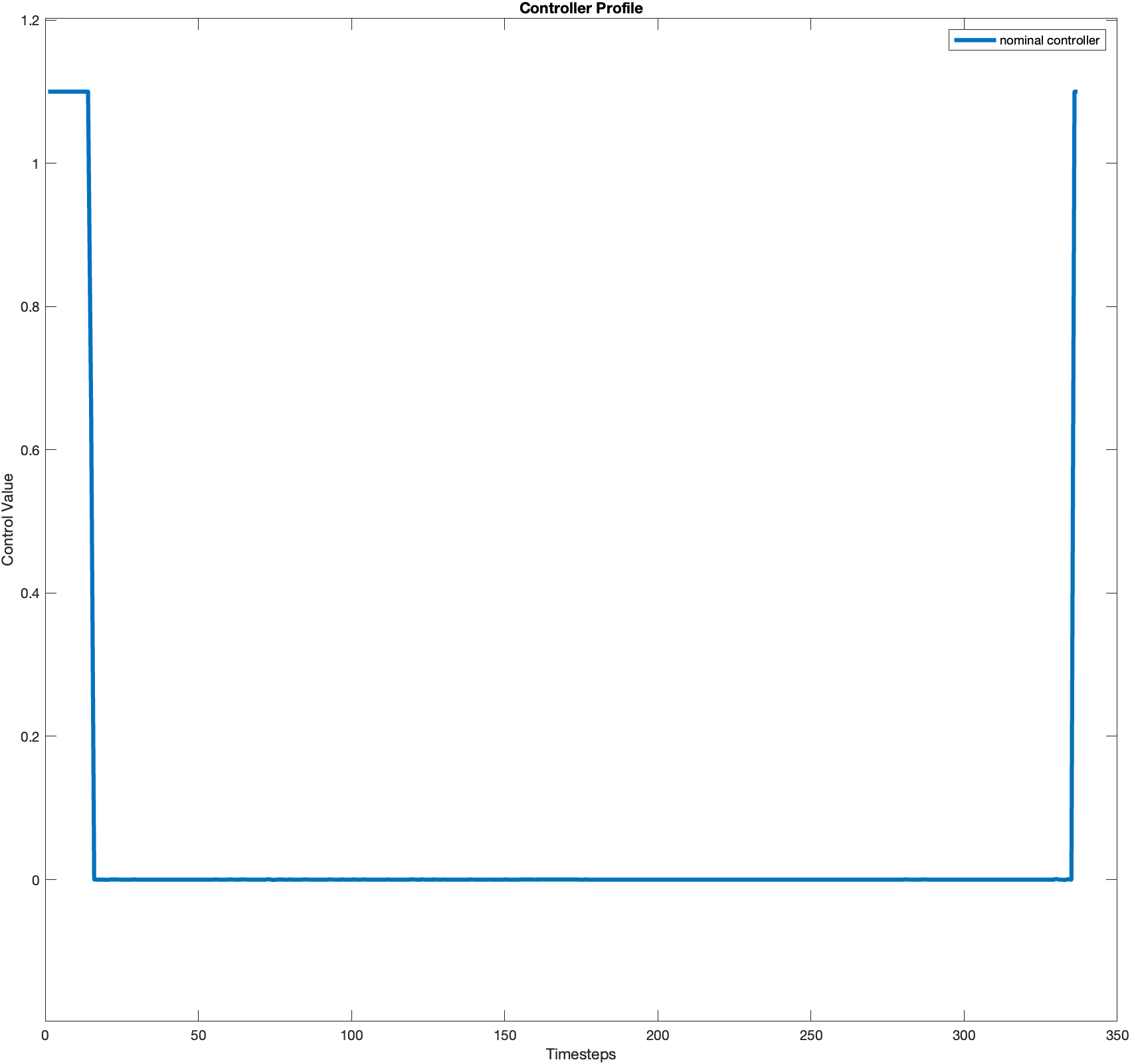
Part 4
Test case 4
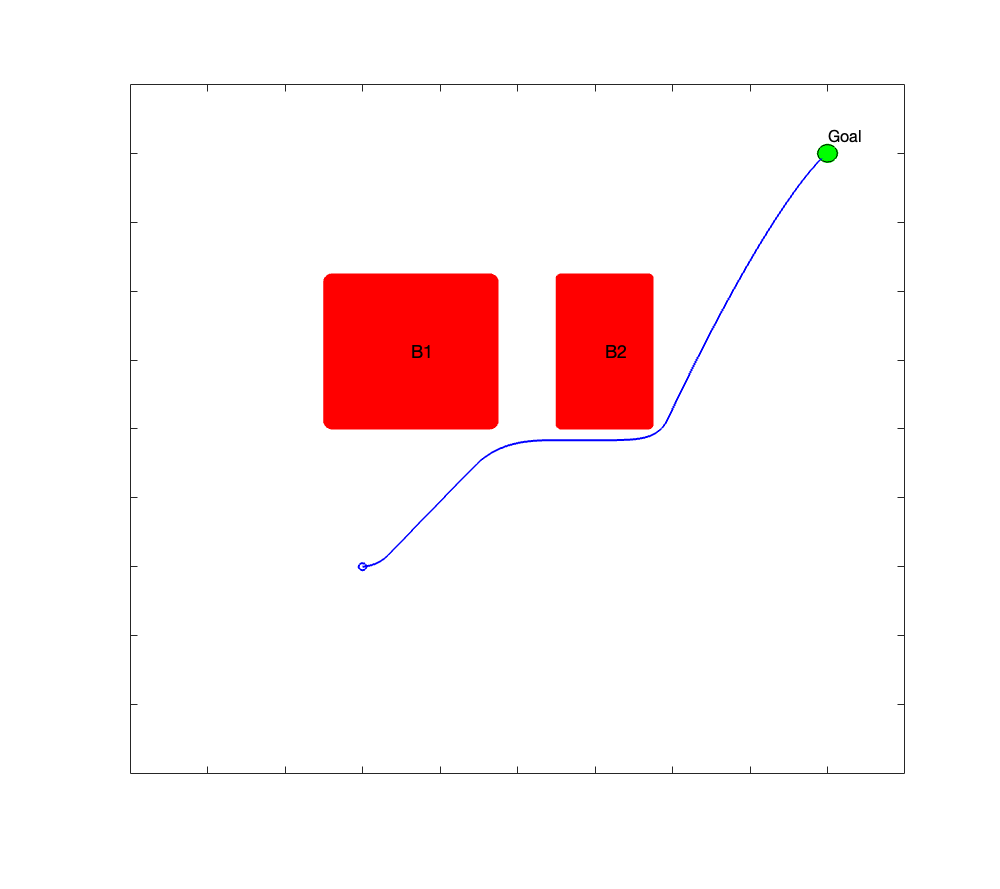
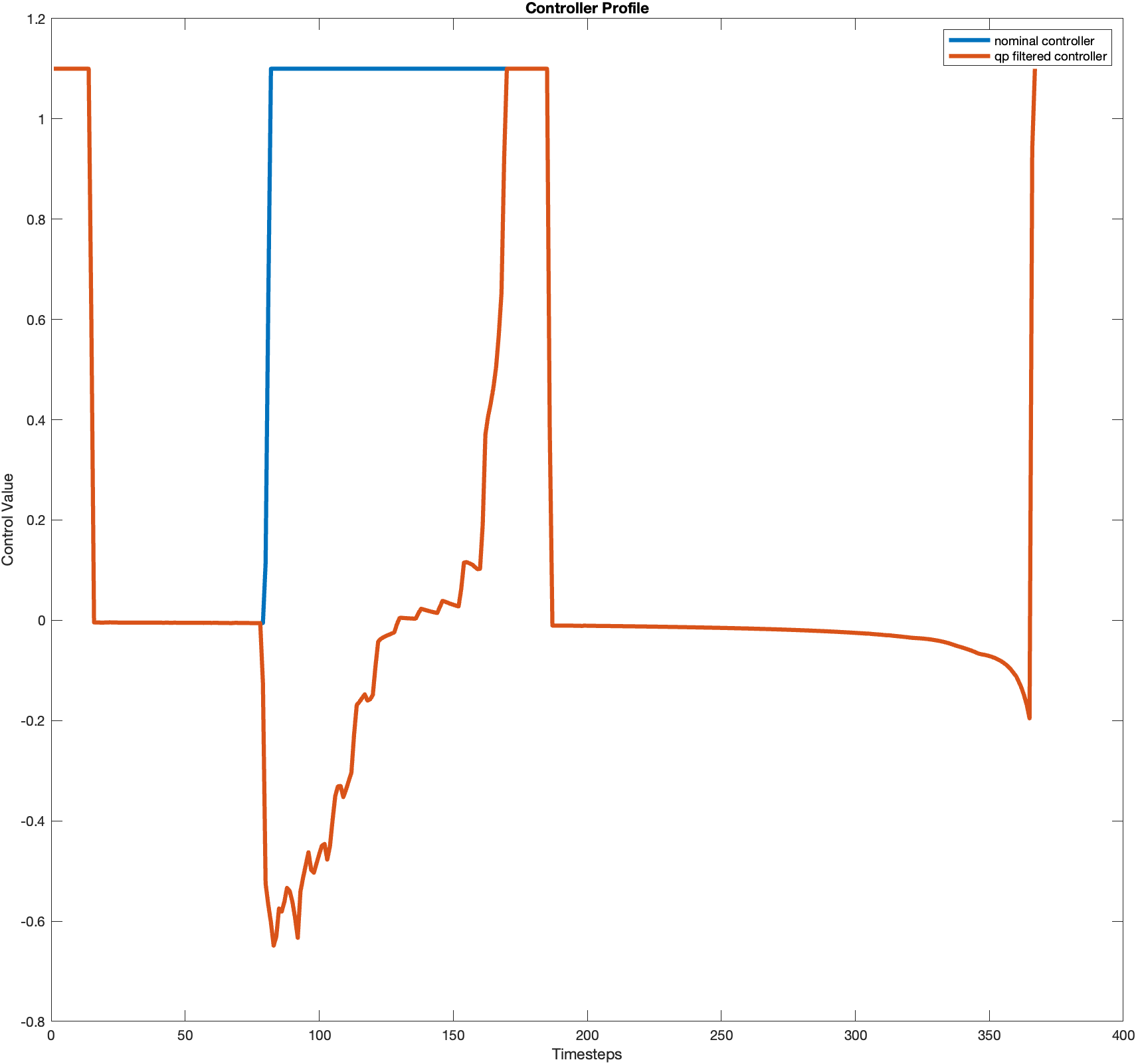
Test case 5
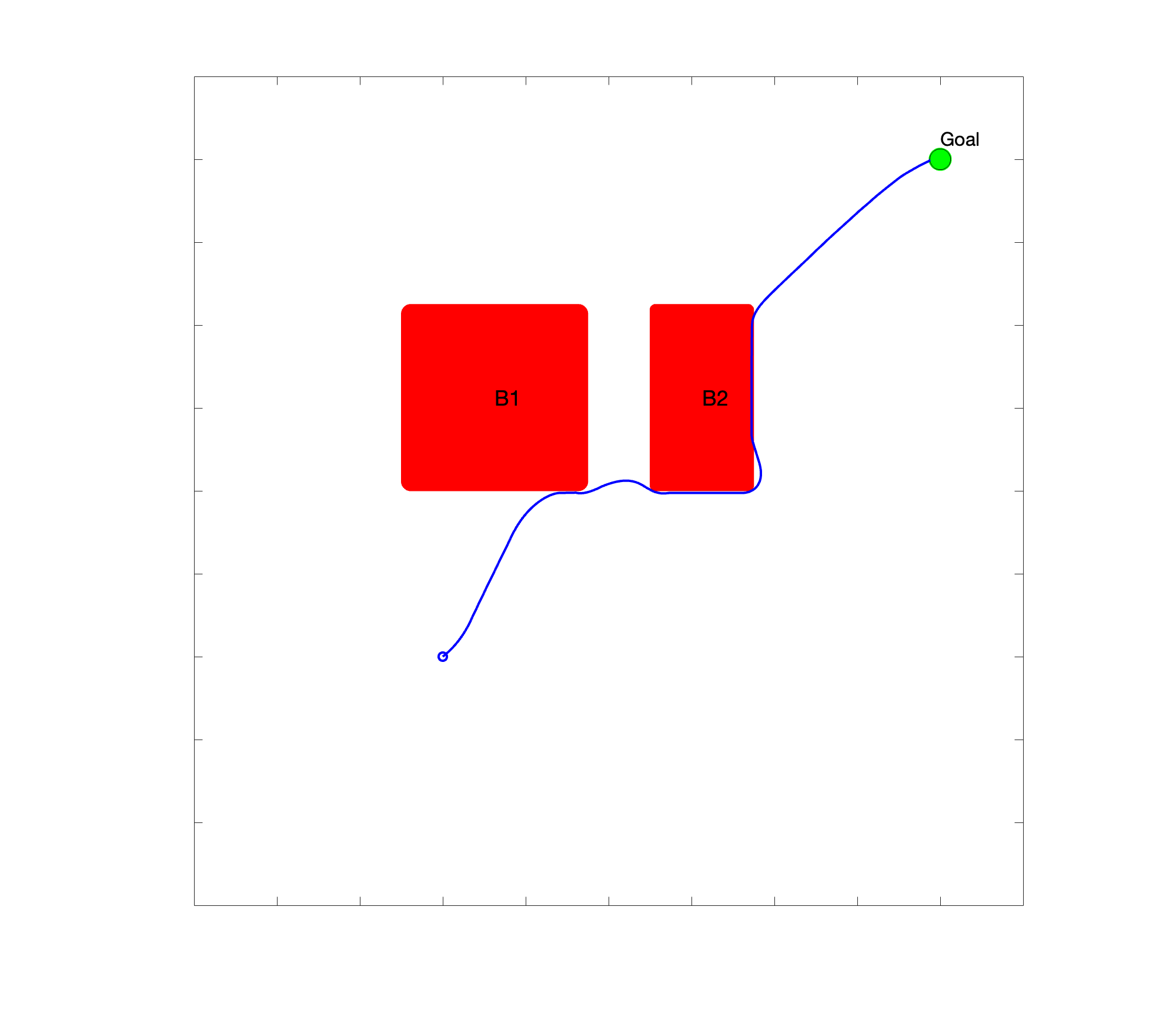
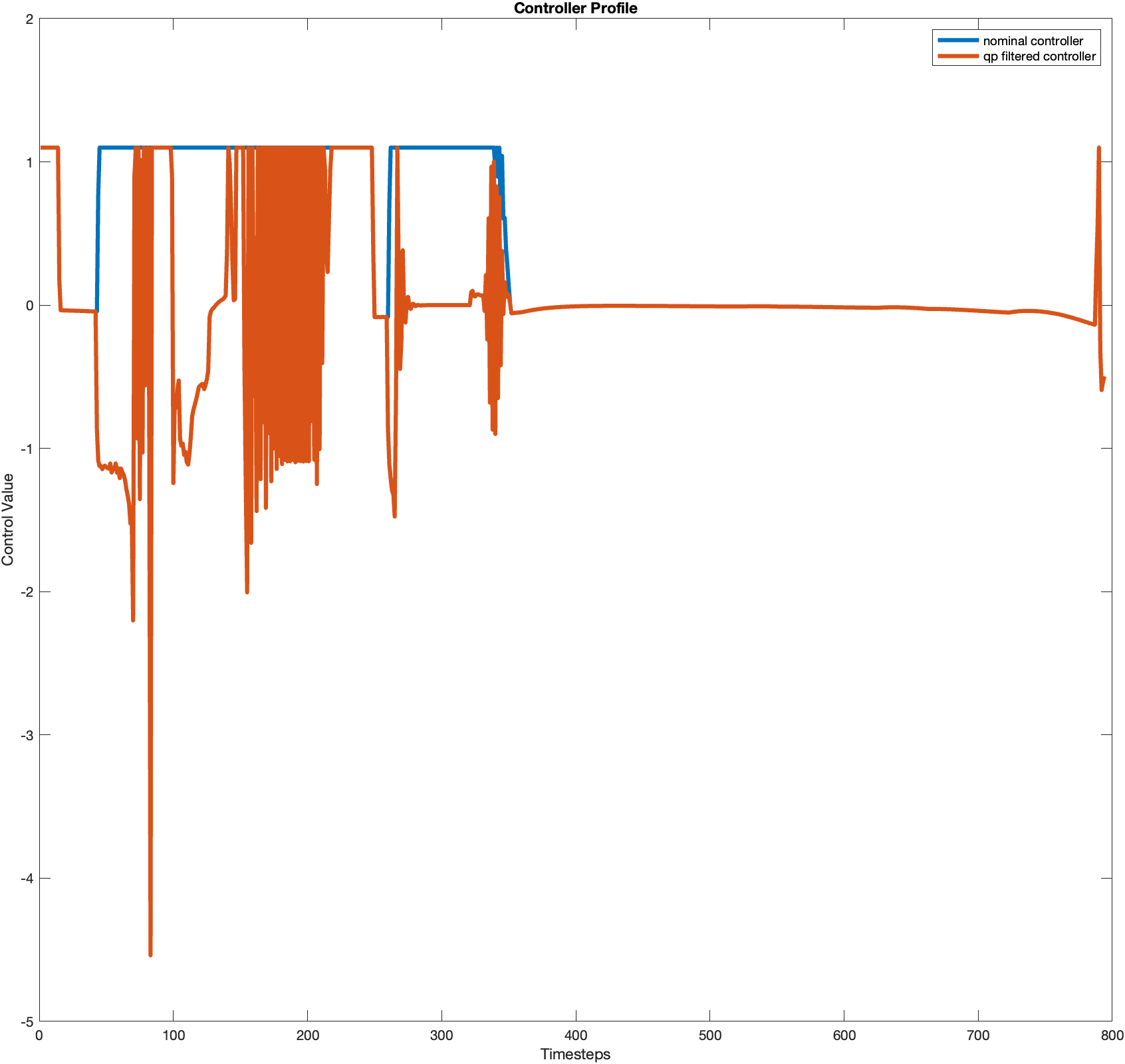
QP Code
%% TODO
% Code in the quadratic program that implement the QP
% min(u) 0.5*||u_nom -u||^2 st u is a safe control
A = -dvdx(3)*params.dt;
b = valuex+dvdx(1)*(cos(current_state(3))+params.speed)*params.dt+dvdx(2)*(sin(current_state(3))+params.speed)*params.dt + ...
params.dt * dvdx(1) .* optDst(1) + params.dt * dvdx(2) .* optDst(2);
u_qp_filtered = fmincon(@(u)0.5*(u-u_nom)^2, u_nom,[A],[b], [], [], [], [], [], options);
The control is smoother than that of part 3, demonstrated by the control profile.