Four Models

---

Possible Real-life Meanings of $X$ - Random Variable

• Time to event
• Survival time after cancer diagnosis
• Time in remission
• Recovery time after surgery
• Dollar amount of an auto insurance claim
• Dollar payment on a medical malpractice policy in one year
• Number of claims submitted in six months

---

Cumulative Distribution Function (CDF)

Definition

The cumulative ditribution function is also called the distribution function. It is usually denotes as $F_X(x)$ or $F(x)$, for a random variable $X$. It represents the probability that $X$ is less than or equal to a given number. That is $F_X(x)=\mathrm{Pr}(X\le x)$. The abbreviation cdf is often used.

$$F(x) = \mathrm{Pr}(X\leq x) = F_X(x)$$

1. $0\leq F(x)\leq 1$

2. Non-decreasing

3. Right-continuous $\displaystyle \lim_{x \to x_0^+}F(x)=F(x_0)$

4. $\displaystyle \lim_{x \to- \infty} F(x)=0$, $\displaystyle \lim_{x \to \infty} F(x)=1$

---

Survival Function

Definition

The survival function, usually denoted as $S_X(x)$ or $S(x)$, for a random variable $X$ is the probability that $X$ is greater than a given number. That is,

$$S(x)=1-F(x) = \mathrm{Pr}(X>x)$$

1. $0\leq S(x)\leq 1$

2. Non-increasing

3. Right-continuous $\displaystyle \lim_{x \to x_0^+}F(x)=F(x_0)$

4. $\displaystyle \lim_{x \to- \infty} S(x)=1$, $\displaystyle \lim_{x \to \infty} S(x)=0$

Exponential Survival Function

$$\begin{equation} S(x) = \left\{ \begin{array}{lr} 1, & x < 0 \\ e^{-x/\theta}, & x\ge0 \end{array} \right. \end{equation}$$

---

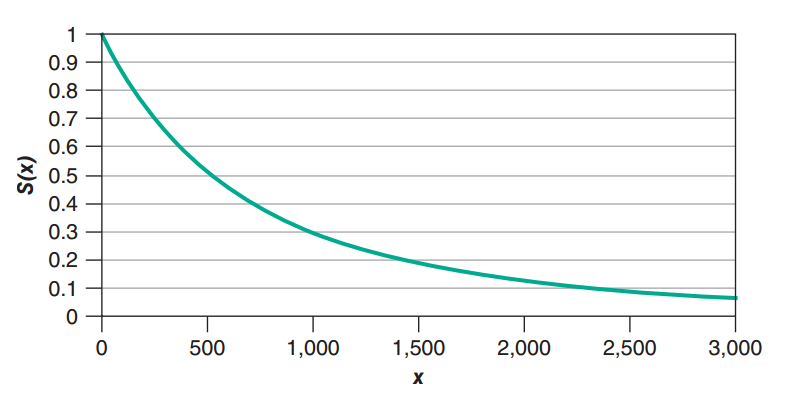
Probability Density Function (PDF)

$f(x) = F'(x) = -S'(x)$ if derivative exists

---

Hazard Function

$h(x) = \frac{f(x)}{S(x)}=\displaystyle \lim_{\delta \to 0} \frac{\mathrm{Pr}(x<X<x+\delta)/\delta}{\mathrm{Pr}(X\ge x)}=\displaystyle \lim_{\delta \to 0}\frac{1}{\delta}\mathrm{Pr}(x<X<x+\delta|X\ge x)$

$h(x) = \frac{f(x)}{S(x)} =\frac{-S'(x)}{S(x)}=-\frac{d}{dx}\ln S(x)$

$S(x) = e^{-\int_{0}^{x}h(t)dt}$

• Cumulative Hazard

  $\Lambda(x) = \int_{0}^{x} h(t)dt$